Graph evolution

Through the first half of the 20th century evolution was mostly the science of selection and splitting. To illustrate with diagrams, a simple selection operation looks like this:

	->		->

...and splitting looks like this:

	->		->

Then in the 1960s, symbiosis and sex started to look as though they needed another fundamental operation - merging - which looks like this:

	->		->

These are the basic operations in modern evolutionary theory. As you can see from the diagrams, these basic operations are particulate - in that they operate on discrete, particle-like entities.

With the modern expansion of the domain of evolutionary theory it seems to me that we need to consider some other levels of analysis. In particular I think we should be thinking about graph evolution and tree evolution. I mean "graph" in the sense of graph theory. You could also call it 'network evolution'.

I'm thinking that a node-and-link scheme would be a better match for the evolution of brains, tree branches, circulatory systems, immune systems, respiratory systems - and so on.

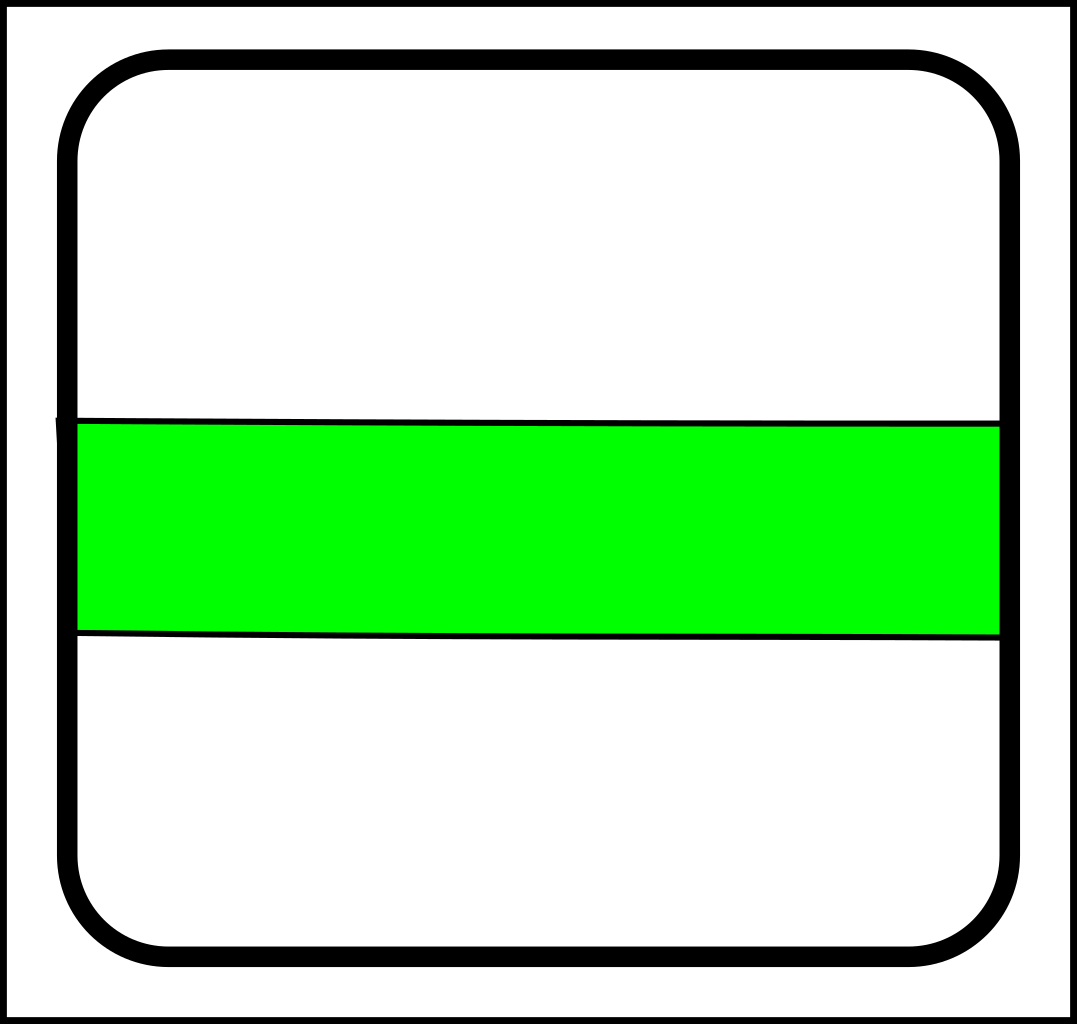
At first glance, this might seem like a case of adding operations that create and destroy links between nodes. That might make sense in computer science, but in nature, links form gradually and a more gradualistic scheme seems more in tune with existing evolutionary theory. Here are the splitting operations:

	->

	->

	->

	->

	->

	->

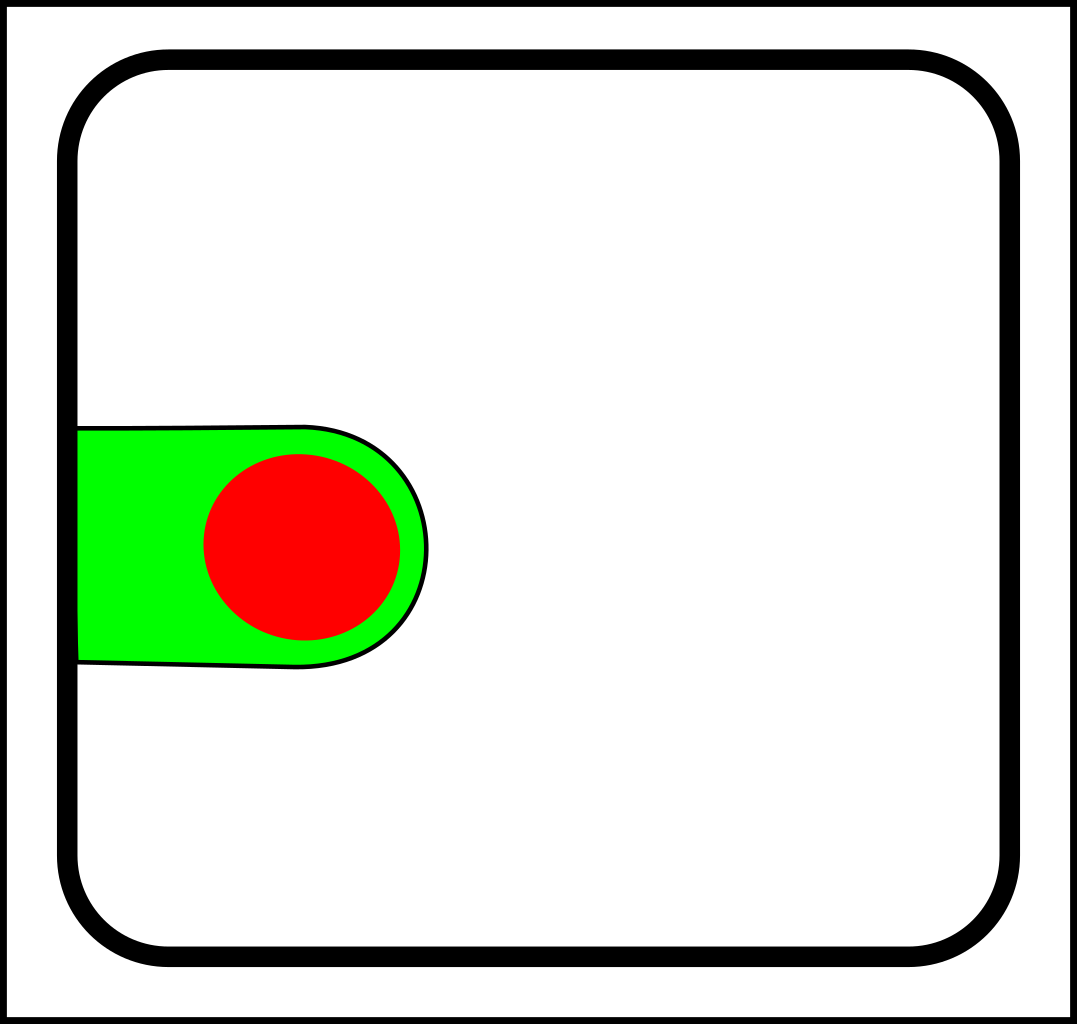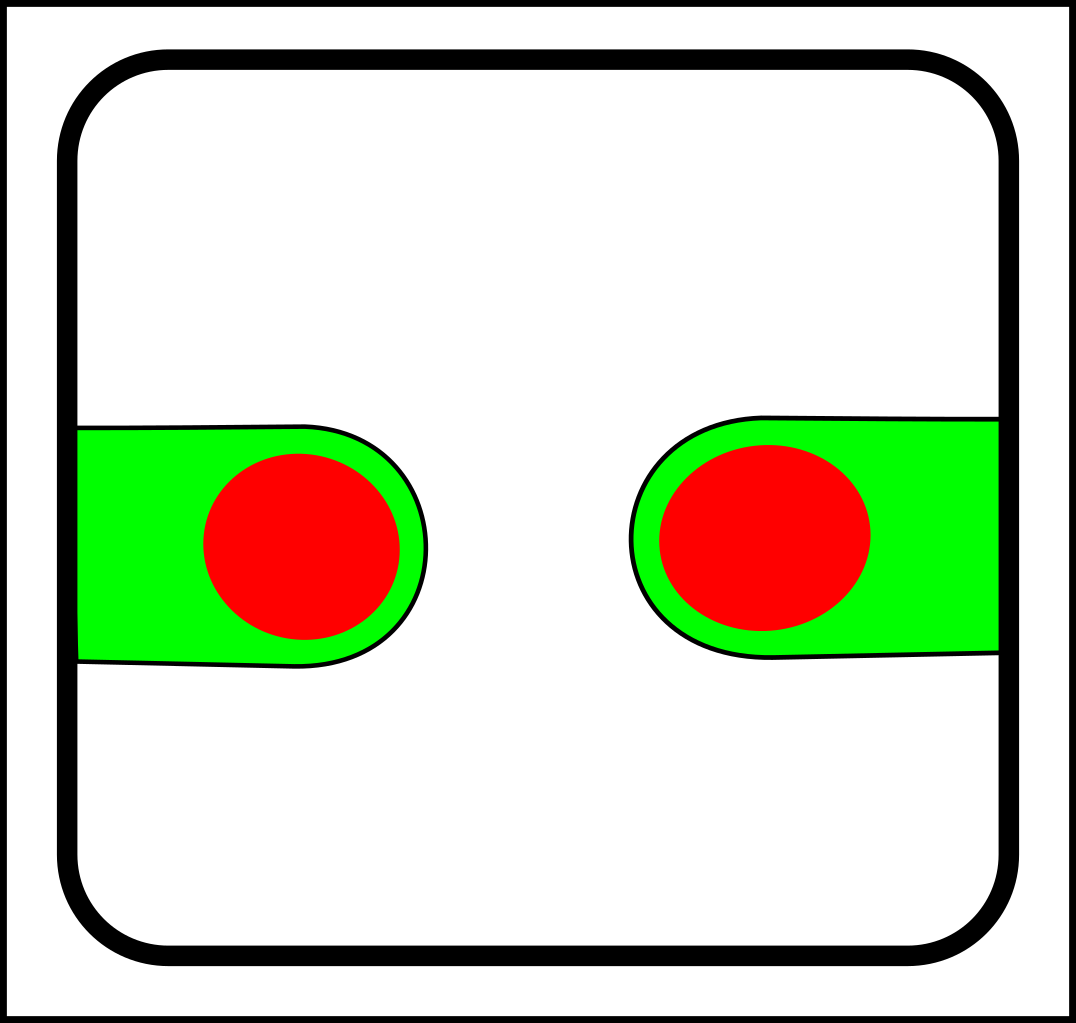
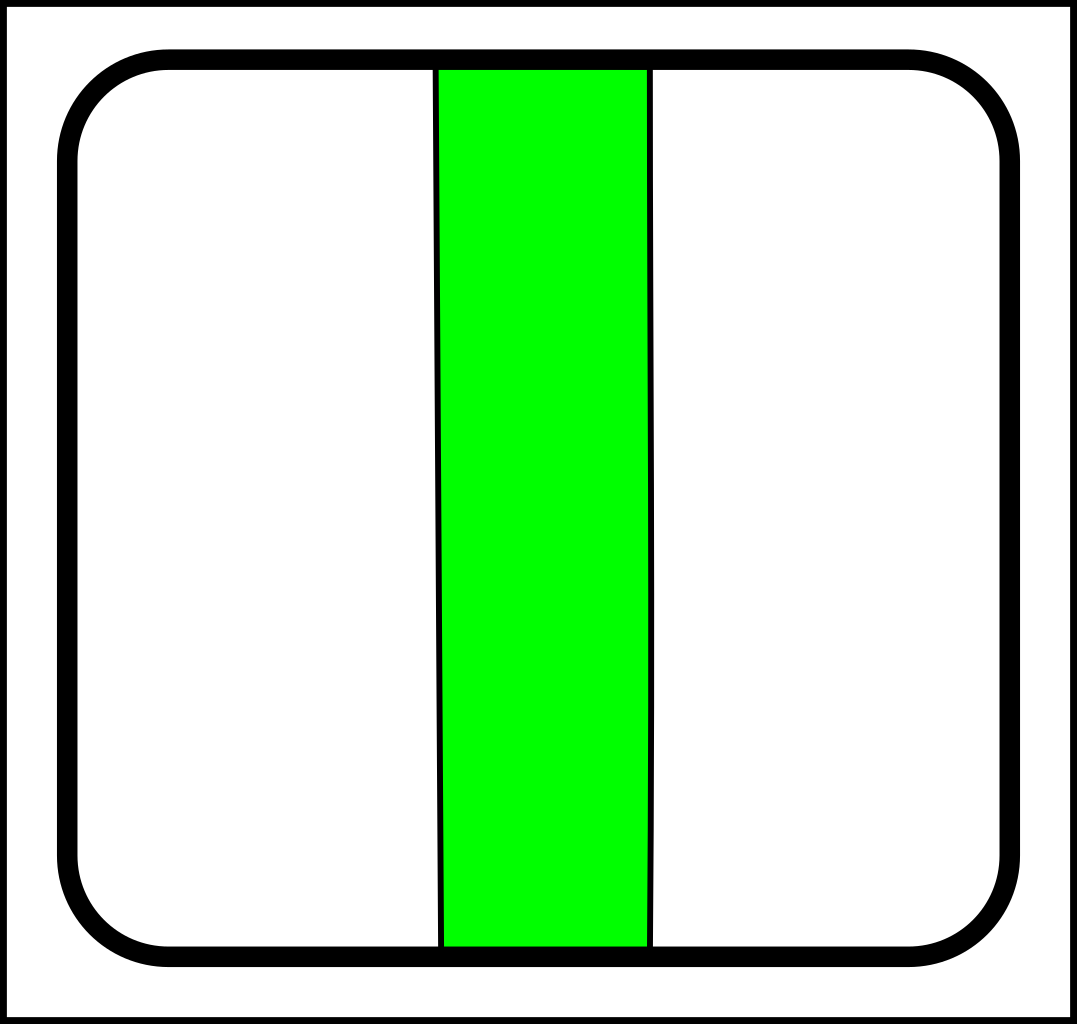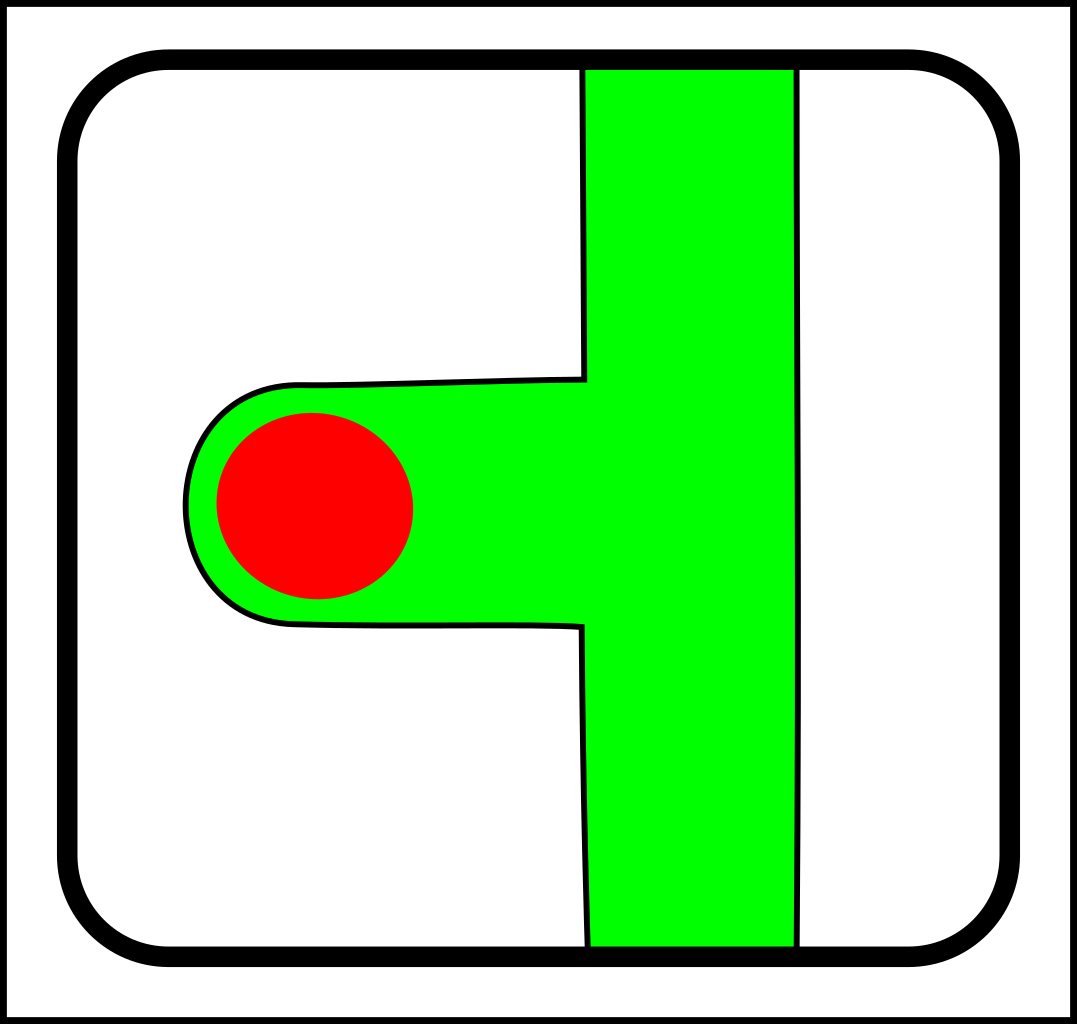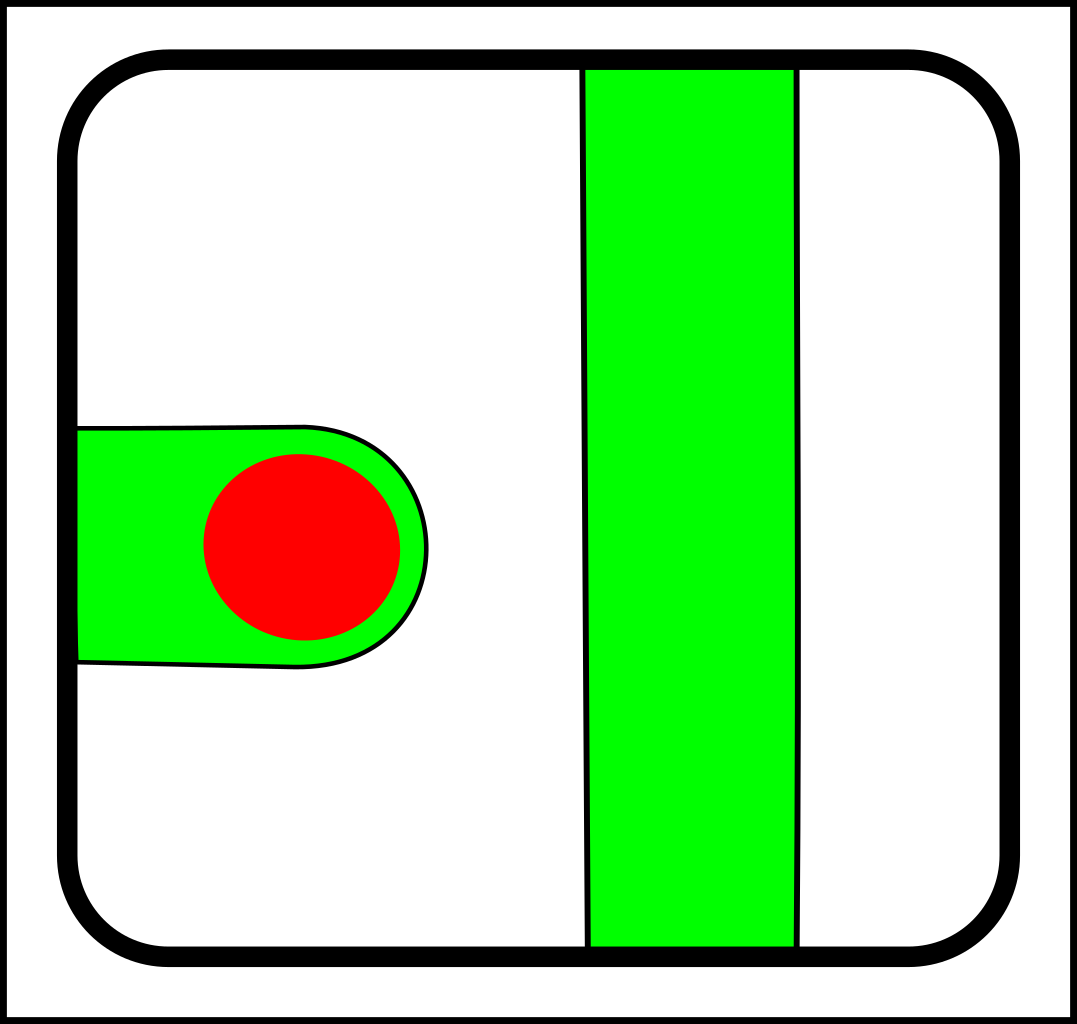
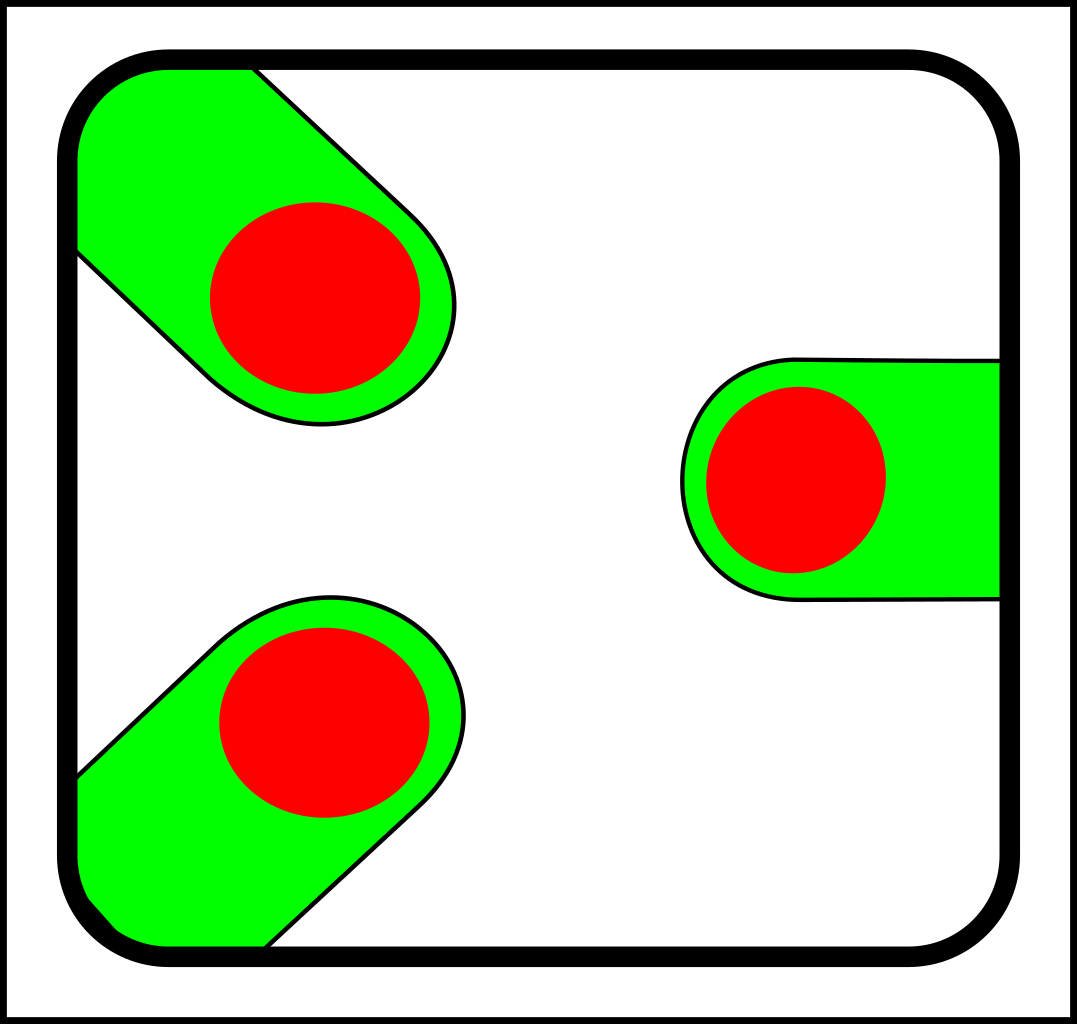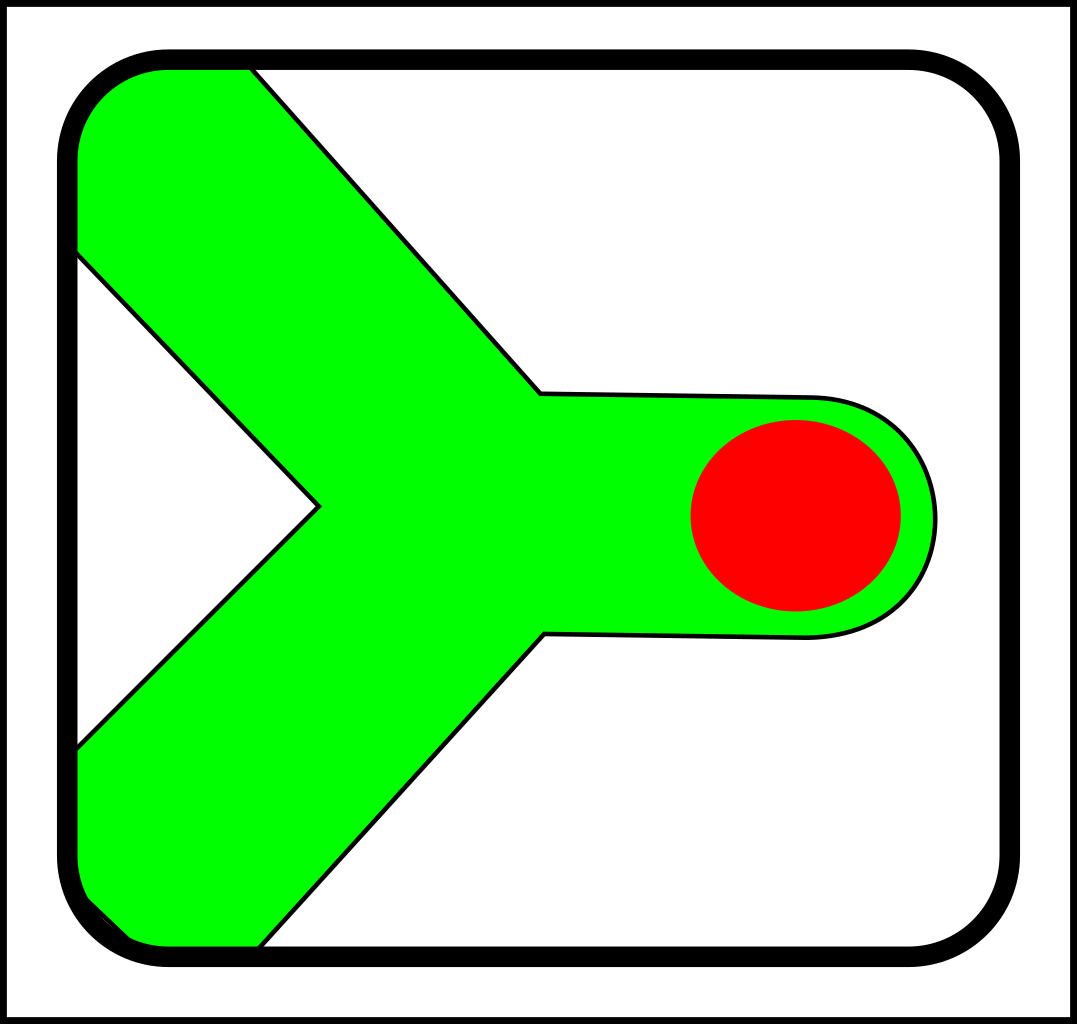
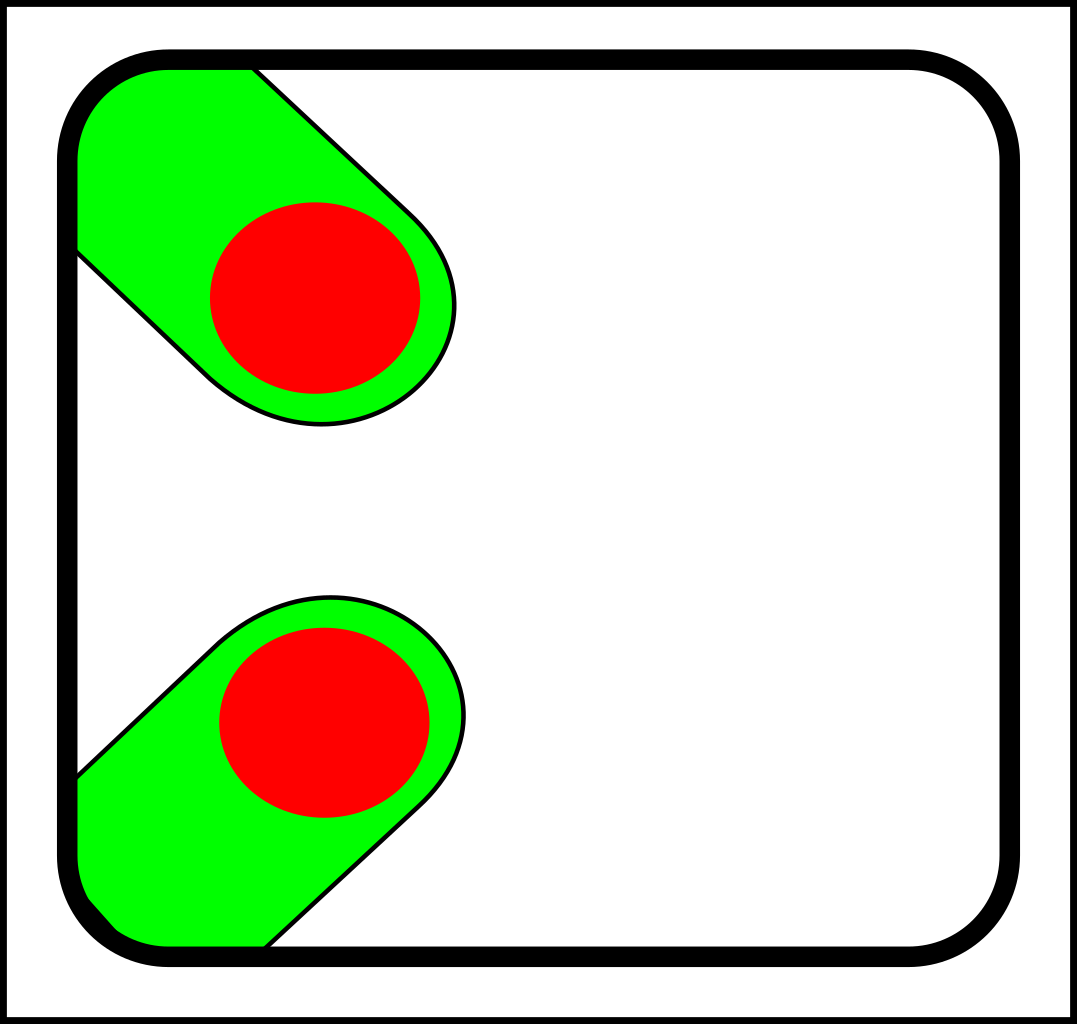...and here are the corresponding joining operations:

	->

	->

	->

	->

	->

	->

For the sake of simplicity, I've only shown diagrams for nodes with fewer than four links. I've also omitted selection events - i.e cases where elements (nodes or links) are simply destroyed.

I should probably say a bit more about the motivation for such a scheme. In biology, tree and graph evolution is often reducible to particle evolution - since the components involved are often composed of particulate cells. However, this doesn't work so well for brain evolution - since axons and dentrites are so link-like.

It's often possible to model branch tip evolution using conventional Darwinian models which treat branch tips as individuals. This works quite well in many of the types of inanimate systems considered by Darwinian physics, for example. However this approach works best when flow into the resulting tree-like structures is time-like - i.e. unidirectional and at a constant speed. If resources can flow back out of unpromising roots or newly-shaded branches, conventional Darwinian models based on a population of branch tips do not work so well. Then, more sophisticated models can be useful.

There is a field called evolutionary graph theory - but that seems to be about something rather different from the topic of this page.