Selection is simple, general and explains goodness of fit

The concept of "selection" is at the heart of evolutionary theory. Some people assign that role to natural selection - but the main difference between selection and natural selection seems to be the idea that selection also includes artificial selection. However, the whole idea that selection by man is somehow "unnatural" doesn't deserve much in the way of scientific respect.

The definition of "selection" in a scientific context is the subject of some controversy. To give an example, Hull, Langman and Glenn (1999) define 'selection' as follows:

we define selection as repeated cycles of replication, variation and environmental interaction so structured that environmental interaction causes replication to be differential.

For me, such definitions are problematical. "Selection" is an ordinary English word, which means "a choice from alternatives". Choosing from alternatives strikes me as being a simple and sensible scientific concept. However, the idea of structured "repeated cycles of replication, variation and environmental interaction" is long-winded and complex. I generally favour simple scientific concepts on basic grounds of parsimony.

It is quite common for definitions of natural selection to be very specific. For example, they often mention "populations" or "inherited traits". Being overly specific is a common problem in science. Scientists favour general theories that explain lots of data over more specific ones that don't explain so much. However while inductive inference proceeds from specific examples to general theories, it sometimes takes a while for it to get there. Selection takes place between alternatives. The term "population" carries with it a lot of irrelevant and unnecessary baggage. As for selection involving "inherited traits" - that excludes selection that acts on traits that are not inherited. Yet much the same theory applies to these traits. Defining selection - or natural selection - as involving "inheritance" is a narrow and blinkered approach to the topic.

The idea of choosing from alternatives is really a very general one. If you think about it, practically any form of change can be described as being the result of a selection between different types of possible change. Selection is often contrasted with mutation - but even mutations can be described as a form of choice - a choice between different possible types of mutation. In evolutionary biology selection of which organisms die, which organisms reproduce and which organisms are chosen as mates are considered to be important forms of selection - while selection of which mutations take place and which do not is not generally considered to be a form of "selection" at all. The "selection" criteria for mutations is often assumed to be pretty trivial: mutations are chosen "at random".

Does the generality of the concept of selection make the concept any less scientific? If practically any change can be explained in terms of selection, then isn't invoking selection as an explanation vacuous? Not really: scientific explanations usually say what type of entities are being selected. An explanation invoking selection on organisms can be perfectly scientific and testable. Specifying the entities being selected in a theory rules out a wide range of other selective explanations. Also, an explanation in terms of selection is always possible - but it might not be likely: other explanations might be more parsimonious. Compare with information. You can describe anything in terms of information. However we still have useful theories associated with information. Being very general is not necessarily a fatal flaw.

In biology, selection is the primary explanation of adaptation. However, goodness of fit is invoked in other areas of science - and very often selection is involved in its creation. For example, observation selection explains goodness of fit between observers and the universe they observe.

There's a grand thesis associated with selection in which selection explains most goodness of fit. Gary Cziko and Donald Campbell are among the proponents of this view. For example, they describe learning strategies as either "instructional" or "selectionist" and then argue that what looks like instructional learning often turns out to be selectionist. This view also has its critics - who describe the act of labeling "instructional" learning as being really "selectionist" as obtuse. For example, Henry Plotkin raises this objection in Evolutionary Worlds Without End.

My sympathies lie with Cziko and Campbell on this issue - though I have some issues with their presentation. It's better to have a broad concept of selection - and this leads naturally to a grand unified theory of selection in which selection explains most goodness of fit. The idea means that selection must be involved in all template copying. For example, the "goodness of fit" between a footprint in the sand and the corresponding foot must be explicable in terms of selection acting against the grains of sand that were displaced. This is a somewhat counter-intuitive use of the term "selection" - but it perfectly possible to imagine the foot as the selecting agent and the grains of sand as being the selectees.

The existence of goodness of fit usually means that - at some stage a selector has acted on alternative choices - and those remaining 'fit' the selector. Of course goodness of fit by chance is always a possibility. However it is a possibility that is usually easily quantified and rejected. Almost all goodness of fit in nature can be attributed to selection.

Fitness landscapes and positional inheritance

Fitness landscapes are a common way of visualizing the relationship between variables associated with an organism and fitness. The height of the landscape represents fitness and the domain over which the fitness landscape is defined is composed of other variables associated with the organism. Most frequently the information associated with heritable elements is used - but other variables affecting fitness could be included as well - such as environmental factors.

In this post, we will apply the idea of fitness landscapes to simple systems involving positional inheritance. Hopefully this will help to illustrate how the concept of 'fitness' applies to these kinds of system. To create a plot of fitness, we have to say what we mean by fitness. Fitness is a notoriously overloaded and slippery idea in biology - as was once explained in a book chapter titled "An Agony in Five Fits". Here, we won't proscribe any particular definition of fitness, but rather will show how to apply some common definitions of fitness.

The first aspect of measuring fitness is to define what entities you are measuring the fitness of. If there are multiple types of organism in a system, you have to say which one you are interested in tracking the fitness of. In simple systems involving positional inheritance this decision is often relatively simple: since there's only one main candidate entity. For example, with lightning strikes tracking the reproducing tips of the lightning are the obvious candidate. With stream systems, the branching tips of the streams themselves would be the most obvious object of study. With propagating cracks, the crack tips would be the object of study. With diffusion-limited aggregation, the available aggregation points would be what was tracked. In many of these cases, the precision of the available measuring instruments may be a factor in deciding exactly what entities are tracked.

Having selected the entities to be measured, the next thing to do is to decide how to measure fitness. Although there are many fitness metrics used for different purposes, we can categorize them in a few main ways. Fitness metrics can be:

• Relative or absolute - depending on whether you are interested in relative success or absolute results;
• Expected or actual - actual fitness measure growth rates while expected fitness can be calculated in advance;
• Short or long term - the time horizon affects fitness measurements: offspring don't always result in grandchildren;
• Generational or per unit of time - measuring growth in generational time units can sometime be useful.

These all apply to positional inheritance systems - though generational measures of fitness are not much use there. It's like using generational fitness metrics with bacteria. Bacteria are mortal and do have lifespans - but their lifespans are not much like the human three score years and ten. It's more a case that the bacteria live until they have a fatal accident - and the frequency of bacterial deaths are heavily determined by environmental factors. Thus, the lifespan of a bacterium is not usually a particularly useful or interesting figure. Using generational fitness with simple positional inheritance systems is a lot like this.

A fitness landscape is usually a plot of fitness over gene space. The peaks illustrate where well-adapted organisms are likely to be found. The roughness of the fitness landscape influences whether and how quickly evolving organisms will be able to find the peaks.

With simple positional inheritance systems, the 'genes' in question are positions - since position is one of the main things that is inherited in these systems. So the domain of the fitness landscape plot is usually simple two or three dimensional space. Fitness measures how likely branching or splitting is to take place at points in that space. Since reproduction typically requires resources, fitness can be reasonably expected to be correlated with resource availability.

It is common for fitness landscapes to change over time. As the environment changes, different genetic combinations are favored - and the fitness landscape shifts dynamically. With simple positional inheritance systems fitness landscapes tend to change in a predictable manner - the highest peaks tend to be systematically eroded. Because reproduction requires resources, takes place where resources are plentiful and depletes local resources, resource-rich areas will be systematically exploited and eliminated.

Fitness landscapes only track the parameters specified in their domain. If other factors affect fitness, the calculated fitnesses will not be accurate if these are omitted. For example, it is common to leave environmental factors out of fitness landscape plots.This can result in a lack of realism. With simple positional inheritance systems, fitness can also depend on more than positional factors. For example, consider a spreading fire. The reproduction rate of flames will be heavily influenced by positional factors - such as the local availability of combustible material. However other factors can also affect the rate of flame reproduction - such as the wind direction and the temperature - these are often a function of time as well as position. If there are more factors you can add them to the domain of the fitness landscape - but then you get a more complex plot in a higher dimensional space - which might not be so easy to make use of.

References

• Tyler, Tim (2012) Positional inheritance
• Tyler, Tim (2012) Positional inheritance (video)

Richard Dawkins on memes, Oxford, 2014

The blurb reads: An extract from Richard Dawkin's open Q&A session at the Oxford Union on 18th February 2014.

I think this talk illustrates replicator rot. IMO, this conception of a meme is a dead end and isn't suitable for use as the basis of a science of culture. However, we don't have to define memes in the exact same way as Dawkins.

C.G.P. Grey explains memetics

C.G.P. Grey explains memetics in terms of "thought germs" in the following excellent video titled "This Video Will Make You Angry":

Notable previous videos from C.G.P. Grey include:

• Humans Need Not Apply (Automation)
• This Video Will Hurt (Nocebos)

I suspect that the content of "This Video Will Make You Angry" was inspired by Scott Alexander's essay The toxoplasma of rage - which came out a few months earlier and covers much the same topic.

George Price: pioneer of Universal Darwinism

George Price should get considerable credit for pioneering the idea of what we now call Universal Darwinism. Here's George:

Selection has been studied mainly in genetics but of course there is much more to selection than just genetical selection. In psychology for example trial-and-error learning is simply learning by selection. In chemistry, selection operates in a recrystallisation under equilibrium conditions, with impure and irregular crystals dissolving and pure, well-formed crystals growing. In paleontology and archaeology selection especially favours stones, pottery, and teeth and greatly increases the frequency of mandibles among the bones of hominid skeletons. In linguistics selection unceasingly shapes and reshapes phonetics grammar and vocabulary. In history we see political selection in the rise of Macedonia Rome and Muscovy. Similarly economic selection in private enterprise systems causes the rise and fall of firms and products. And science itself is shaped in part by selection with experimental tests and other criteria selecting among rival hypotheses.

This is from Price's posthumously-published 1995 manuscript, "The Nature of Selection". Price went on to lament the lack of a proper theory of selection and the lack of a proper definition of selection. He compared the current state of selection theory with the state of information theory in 1922. Price died in 1975 and apparently this paper was written in 1971 - which makes it ahead of its time indeed. Extensive quotes from "The Nature of Selection" are available free online - in the paper George Price's Contributions to Evolutionary Genetics.

While things have moved on a bit since 1970s the theory of selection is still little known. Evolutionary theory should cover it - but hardly anyone seems to realize that the theory applies to physical systems like crystals in the way that Price clearly indicated. Evolutionary theory is still in an immature state, where it isn't applied through much of its rightful domain. Progress is pretty treacle like: Darwinism has a pretty huge inertia. Also there are fragmented areas of science that are part of the study of selection that are scattered all over the place. Observation selection seems to be studied mostly by physicists and links to evolutionary theory are mostly ignored. Selection bias and sampling effects are concepts which are widely used in science - but again, these topics are rarely seen as being in the domain of evolutionary theory.

Parent-offspring asymmetry

In evolutionary processes, sometimes parents and offspring are indistinguishable and other times, they are very different.

Newborn human offspring are very different from their parents. They are much smaller and more helpless. By contrast, bacteria generally reproduce via binary fission - and parent and offspring are identical. DNA molecules produce offspring DNA molecules where it makes no sense to ask which molecule is the parent and which is the offspring.

In cultural evolution we also have a mixture of parent-offspring symmetry and asymmetry. Copies of the GPL are mostly identical and they spread via cloning rather like a virus. By contrast, many complex human memeplexes undergo a developmental process within the human mind. It is usually pretty easy to distinguish between the memes in the teacher and the memes in the student: the student's memes are less mature and well developed.

I think whether that newborn offspring identical to their ancestors (or not) is a reasonable classification criterion for evolutionary entities.

However, there can sometimes be some issues. For example, sometimes what seems to be a newborn which is identical to its parent can - on closer inspection have some systematic differences. FOr example, with DNA strands there is a parent-offspring relationship: the 'parent' strand is used as the template for the formation of the 'offspring' strand. However, this relationship is not obvious unless the copying process itself is witnessed. Once the copy has been made it is hard to distinguish it from the original - unless the copying fidelity involved is poor.

A similarly problematical example from the cultural realm is photocopying. A photocopy might appear to be identical to the original document. However a detailed examination will probably reveal some differences - allowing the original to be distinguished from the copy.

This issue is an imperfection in this classification scheme - but hardly a terminal one. It is useful to distinguish between organisms that develop significantly after birth from those that do not.

The reproductive resource gap

It's a commonplace observation that reproduction requires resources.

Reproduction often creates a transient, local resource depletion that decreases the chance of future reproduction in the short term. This "reproductive resource gap" is the topic of this article.

I've long known about this "resource gap". It seems to apply to many organic and cultural systems. Recently, I have been thinking about how general this principle is. It clearly doesn't apply to all creatures. For example a termite queen doesn't have a measurable reproductive gap - her reproductive system is a pretty continuous assembly line. However, for many creatures - from bacteria to elephants, there is a "reproductive gap" - where the mother has to accumulate resources after splitting and before splitting again.

Splitting typically produces offspring which are smaller than the mother. One hypothesis is that size is responsible for part of the effect - that bigger things are more likely to split than smaller things.

However, we know that - in many cases, the reverse relationship holds - i.e.: smaller things are more likely to split than bigger things are.

This is true for most organisms in the biosphere: there's a strong negative correlation between an organism's adult size and their reproductive rate. Smaller critters reproduce faster.

It's also true of very large objects. For planets and stars, smaller objects are more likely to break up than larger ones are - because the larger ones are held together more effectively by gravity.

Also, if erosion or corrosion are involved in the splitting - then these forces apply to the surface of objects - so again, small objects would be more strongly affected - because they have relatively larger surfaces.

Another perspective on the issue comes from considering a simple, common case. Some of the most common particle interactions in the universe consist of photons hitting dust particles. The photons form a a clear family tree with a few high energy photons near the root and enormous numbers of low-energy photons at the tips of the branches and a clearly-defined set of branching points - when the photons hit the dust particles and split.

In this system, the distance (or time) from one branching point to the next doesn't increase with proximity to the root. If anything, there's a tendency for collisions to be quickly followed by more collisions (if you just hit some dust there may be more things to hit nearby). This is another case where splitting tends to lead to more splitting - rather than to less splitting.

There are many other cases where splitting leads to more splitting. In a landslide, rocks that lave been stable for a long period of time might suddenly split many times in quick succession. There are many cases where splitting generates jagged edges and jagged edges result in more splitting. Beach pebbles are an example of this. Another similar case involves splitting reducing structural integrity. An egg is the stereotypical example, but similar considerations apply to many structures with membranes or skins. Breaching the outer wall leads to splitting and rapid disintegration.

At this stage a brief recap. A reproductive resource gap seems to be a pretty common feature of organic and cultural evolution - often the mother seems to need time to recharge. This applies to K-Selected creatures - and also to many r-selected ones - such as bacteria. However in many simple physical systems, there's often no reproductive resource gap. Instead, we find the opposite: splitting is likely to be followed by more splitting.

At this stage it might be tempting to conclude that the reproductive resource gap is an adaptation for managing limited resources - and that the reason simple systems don't have a resource gap is that they are degenerative systems which can't accumulate adaptations.

However, I've skipped over presenting some significant data. There are, in fact, simple physical systems that do exhibit a reproductive resource gap. One example involves raindrops in a condensation cloud. Smaller droplets have larger surface area to volume ratios - and so are more likely to be held together by surface tension. Another system involves falling ink droplets in water. The easiest way to explain this is with a video.

The video pretty clearly illustrates droplet reproduction - and a family tree of droplets.

However, there's a characteristic delay between one droplet reproduction event and the next. It is as though the falling droplets need to build up some kinetic energy before they can reproduce again.

In my opinion, these examples demonstrate that the reproductive gap is more than just an adaptation. There's a simple physics of needing to accumulate resources after splitting and before splitting again.

This is, I think, an interesting result in a poorly-studied area. Future investigations into the topic could look into how widespread this "reproductive resource gap" is in simple physical systems and what the interactions are between the simple physics of needing to accumulate resources before splitting and adaptations for resource management in organisms.

Positional inheritance and heritable fitness

One of the commonly-specified requirements for Darwinian systems is that fitness must be heritable. In other words, on average, fit offspring should be ancestral to fit descendants. Without this condition being met, adaptations can't get off the ground.

In this post, I will argue that this requirement is commonly met by many types of simple, natural systems involving positional inheritance.

The thesis here will be that macroscopic variations in resources are common - and result fairly directly in heritable fitness. If resources are very evenly distributed, then the condition that fitness is heritable would not be met. Such extremely even distribution of resources can happen if the environment is near to equilibrium, for example.

With diffusion-limited aggregation systems, the concentration of aggregating particles can be greater in some places than others. In electrical discharge systems, the potential gradients can be greater in some places than others. With propagating cracks, the medium can be more brittle in some places than others. These situations are all commonplace ones.

The existence of heritable fitness is consistent with observed adaptations in these types of systems. Drainage basins are well adapted to rapidly dissipate the potential energy in the incoming rainwater - and form similar structures to drainage systems designed by engineers. Lightning strikes take the shortest path from the cloud to the ground. Cracks seek out lines of weakness - resulting in an adaptive fit between the actual cracks and the weak points of the material.

In practice, the requirement for heritable fitness is a pretty trivial condition which is almost always met. To evolve adaptations some additional, more stringent conditions are also required. Essentially, the selection pressure needs to out-weigh the mutation pressure. If it doesn't do so, you get an error catastrophe - and no adaptations. In other words, devolution - rather than adaptive evolution.

Spend vs save

Resource allocation is best known as a key issue in project management. However, it is quite a general topic - perhaps best seen as being part of systems theory or cybernetics.

This article goes over some basics of how resource allocation theory applies to organic organisms - and then compares this with the situation in cultural realm.

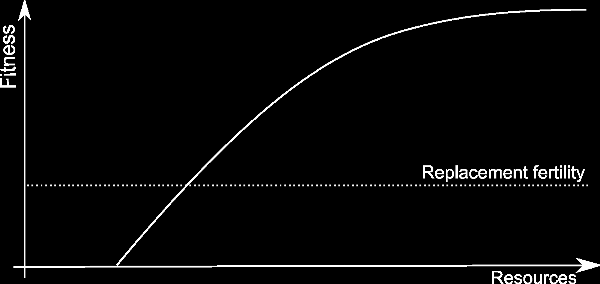Organisms can covert resources into fitness. However they face limits when doing so: too few resources and they can't even live, let alone reproduce; too many resources and the organism can't utilize them fast enough. This situation is illustrated on graph to the right:

The exact shape of this curve is species-specific - some species are better able to take advantage of resources surpluses than others. In particular, r-selected species typically go in for resource storage much less than K-selected ones do.

Environmental resources are not necessarily constantly available. Fluctuations in resource availability result in the need for resource storage. Organisms often need to divide their resources between ones used now and ones saved for later. Sometimes more resources are available than can be utilized at once. At other times, a future resource shortage is anticipated - for example due to the impending arrival of winter. For examples of storing for scarcity:

• Cacti receive water infrequently - and must store it in order to survive when it is absent from their environment;
• Hibernating mammals store energy as fat and then burn through it in the winter.

In the organic realm, resources can be stored as fat deposits, underground tubers, buried nuts, or egg albumen. In the cultural realm, we have stored resources such as batteries, canned food, reservoirs and barrels of oil.

In addition to adaptations associated with actually storing resources, there are also adaptations associated with when to store resources and when to spend them.

Thermostats make good examples of resource expenditure adaptations in the organic and cultural realms. There's a thermostat in your body - that keeps your temperature within a narrow range of values. There's another thermostat in your fridge - which does something very similar. Your building probably contains more thermostats that act to regulate the air temperature. In each case, the availability of resources is largely ignored by the thermostat.

Another important target of expenditure in both the organic and cultural realms is offspring. Surviving offspring are typically expensive - and often organisms only manage to produce one or two. This is an observation that applies broadly to organisms of many sizes - and to both the organic and cultural realms.