On NLP

Looking at what the internet thinks about NLP (Neuro-linguistic programming) suggests that it has decided that NLP is pseudoscience.

NLP was a bit pretentious - by putting the term "neuro" in its name - but we could have lived with that. It is true that humans are programmable animals - and that they can be programmed using language. This is fairly obviously a topic for scientific study.

It seems a bit unfortunate that NLP didn't make more headway. If NLP fades away there will be a bit of a void in the niche it once occupied. I think we should probably hang on to the "linguistic programming" part. I can't think of any more appropriate terminology. We do have the well-established term "suggestion" - but "linguistic programming" is specifically to do with language, and not all "linguistic programming" comes in the form of suggestions.

The problem I see with "linguistic programming" is that you can program both brains and computers with language - but these are pretty different topics, so there is not all that much need for an umbrella term.

The most obvious alternative to this path that I see is to try and hang on to NLP - and turn it into a respectable topic. I'm sure that that path will have some advocates. I'm not sure at this stage that this plan would be effective.

The cultural nose hypothesis

As Richard Dawkins put it in 1976:

Most of what is unusual about man can be summed up in one word: `culture'.

The human nose is an unusual feature of humans. Most apes have flat noses. Does culture explain the human nose? If so, how?

Several hypotheses come to mind. One proposes that big noses come with pronounced brow ridges which act to defend the eyes against being punched in the face - something which humans are much better at than our cousins. Gene-meme coevolution comes in here since accurate punching is tied in with rock throwing skill - which is a culturally-transmitted hunting technique.

Another hypothesis is that the nose acts as an air lock. The nostrils point down, preventing water from entering the nose during common swimming techniques. Swimming is a culturally-transmitted trait. Humans are much more water-friendly than other apes. Water is potentially a strong source of selection, since water entering the lungs can be fatal. Elaine Morgan is probably the best known proponent of this idea. She covers it in her book The Scars of Evolution, for example.

Another hypothesis is sexual selection. Whenever some part of the body grows to an unusual size, sexual selection ought to be on the table as a possible explanation. The nose of the proboscis monkey illustrates this possibility.

Lastly, northerners tend to have bigger noses than equatorial folk - suggesting that the nose acts as a heat exchange and represents one of many adaptations to living in a cold climate - somethings humans can do largely due to cultural transmission.

I tend to favor the 'airlock' hypothesis. The heat-exchange hypothesis predicts that most Africans should have chimp-like flat noses - which they evidently do not. The idea of a defensive barrier would suggest that males would have bigger noses than women. Similarly, sexual selection typically affects traits differently in the different sexes. There is some nasal sexual dimorphism - but probably not enough for these theories.

I propose here that the 'airlock' hypothesis be promoted as the cultural nose hypothesis.

Branch tip evolution

I came up with the idea of branch tip evolution in 2012 by thinking about positional inheritance. Probably the simplest way to understand it is by thinking about the evolution of buds on tree branches. Buds reproduce and they undergo selection. The result is often an adaptive fit between the shape of the tree and its environment. For example, some buds may be in shade under a bridge while others may overhang a busy road. Selection affects the growth and reproduction of the buds, resulting in an adaptive fit between the shape of the tree and its environment.

Copying with selection resulting in adaptive fitness are the hallmarks of Darwinism. However this was not a form of Darwinism based on DNA genes. The example holds up even if all the tree buds involved are precisely identical in terms of their DNA.

A kind of Darwinism of branch tips can be useful in explaining a wide range of tree-shaped structures in nature. In the organic realm, there are branches, roots, corals, circulatory systems, respiratory systems, and branching axons and dentrites. Inorganic tree-shaped systems include electrical discharges, propagating cracks, crystal growth, and drainage basins.

Many models of these types of inorganic system take a functional approach to them - for example, saying that drainage basins form efficient structures for rapidly removing water from landscapes - of that they maximize the production of entropy. From an evolutionary perspective, such models are all very well, but they are all to do with adaptive function. Adaptation is part of evolutionary theory - but it also has another side: path dependence, or historical contingency. Evolutionary theory provides a rationale for adopting a functional perspective in the first place, and it also helps to explain cases where there are deviations from what strict functionalism might predict.

While branch tip evolution is an excellent and important model of many physical systems, it has limitations. In real trees, there is cell reproduction within the branches as well as at the branch tips. Also, there are other cases where branch dynamics are important - i.e. when not all the action in the system is taking place at the branch tips. Finally, real branch tips can sometimes shrink as well as grow. In such cases, the analogy between the real tree and a family tree starts to break down. More sophisticated models involving graph evolution may be a better fit for such cases.

Bonobos: a natural experiment in cultural evolution

Bonobos exhibit a number of human-like traits when compared to common chimpanzees. They are famously more sociable than common chimpanzees. They exhibit a domestication syndrome and have a range of paedomorphic traits. In humans these traits seem linked to cultural inheritance. Paedomorphism gives brains more time to adapt to culture and reduced levels of aggression facilitate cultural transmission. These observations lead to the hypothesis that bonobos have more cultural transmission than common chimpanzees do.

One point which may conflict with this idea is that bonobo brains are significantly smaller than chimpanzee brains - while in humans, culture seems to have made brains larger. Small brains are consistent with the bonobo domestication syndrome, though.

Key data which evaluating this hypothesis depends on involve comparisons of common chimpanzee vs bonobo cultural learning abilities.

There's some comparative data here. It says (on p.27) that bonobos use tools to acquire food much less than common chimpanzees do. Bonobos do have sophisticated social learning skills, though, as Kanzi demonstrates.

If bonobos are more like humans than chimps because they have more culture, then that would be a fantastic discovery from the perspective of students of cultural evolution. It would make bonobos a snapshot of the development of culture in progress - with common chimpanzees providing a baseline.

Trend riding

What people search for varies over time. Copying results in large scale swings in search query popularity due to herd behavior.

If you can quickly create content that matches what people have recently started searching for, you can attract a lot of attention. This approach is known as "trend riding" or "trend following".

Trend riding is a very common technique. People frequently promote their own content on the back of news stories, for example.

The picture for this post illustrates the basic approach. It is content linked to a trending topic (the American election) with an attached advertisement, using memetic hitchhiking.

Talking about memetic hitchhiking, trend riding can be regarded as a special case of this where the memetic linkage between the carrier and the payload is linkage in search space. That's an unusual type of memetic linkage - but it can still be effective. All the usual logic associated with memetic hitchhiking applies in this case.

In fact, as the picture illustrates, content doesn't have to contain the search terms to benefit from the effect. Sometimes, association is enough. That means that the memetic linkage involved can be in virtual worlds created inside brains.

Riding trends can sometimes work better than simply hitch-hiking on popular content. The problem with popular content is that others will have the same idea as you - and your message may get lost among the messages of others. If you can get in early on a rising trend, others may not have identified it yet - resulting in more traffic for you.

Cultural anatomy

If cultures are composed of cultural organisms, what is their anatomy like, and how can they be dissected?

One of the first meme enthusiasts to propose a way of subdividing cultural entities was Douglas Hofstadter, who promoted an "anatomical breakdown" involving the concepts of "bait" and "hook". For more details, see the article: Douglas Hofstadter's contribution to memetics.

In his 2004 book, Ely Asher proposed another "anatomical breakdown" - involving "anchors", "payloads" and "carriers".

The concepts of "promises" "threats", "rewards" and "punishment" also seem appropriate as common components of many cultural creatures. Emotions are often involved in motivating humans to propagate memes, and this basic Pavlovian approach is one of the most common ones.

There's also the genotype/phenotype split to consider. In some cultural creatures there's a well-defined split between what is inherited and its associated products. Such cases typically involve an irreversible developmental program. Think of a cake and its recipe, for example - or server-side software and the web sites they produce.

I think it would be fair to say that cultural creatures come in many varieties, and that it makes sense for some anatomical structures to be domain specific. To give my usual example of different species of culture, FORTRAN programs and origami patterns need not have the same anatomical structures. However, having said that, the search for common anatomical structures in cultural creatures seems like an important one.

In some cases we can classify cultural organs as follows:

• Sensory organs;
• Motor organs;
• Information processing organs;
• Resource processing organs;

Think of robots, for example, for a place where such classification is appropriate. This path gets us into territory already explored by cybernetics and systems theory.

Graph evolution

Through the first half of the 20th century evolution was mostly the science of selection and splitting. To illustrate with diagrams, a simple selection operation looks like this:

	->		->

...and splitting looks like this:

	->		->

Then in the 1960s, symbiosis and sex started to look as though they needed another fundamental operation - merging - which looks like this:

	->		->

These are the basic operations in modern evolutionary theory. As you can see from the diagrams, these basic operations are particulate - in that they operate on discrete, particle-like entities.

With the modern expansion of the domain of evolutionary theory it seems to me that we need to consider some other levels of analysis. In particular I think we should be thinking about graph evolution and tree evolution. I mean "graph" in the sense of graph theory. You could also call it 'network evolution'.

I'm thinking that a node-and-link scheme would be a better match for the evolution of brains, tree branches, circulatory systems, immune systems, respiratory systems - and so on.

At first glance, this might seem like a case of adding operations that create and destroy links between nodes. That might make sense in computer science, but in nature, links form gradually and a more gradualistic scheme seems more in tune with existing evolutionary theory. Here are the splitting operations:

	->

	->

	->

	->

	->

	->

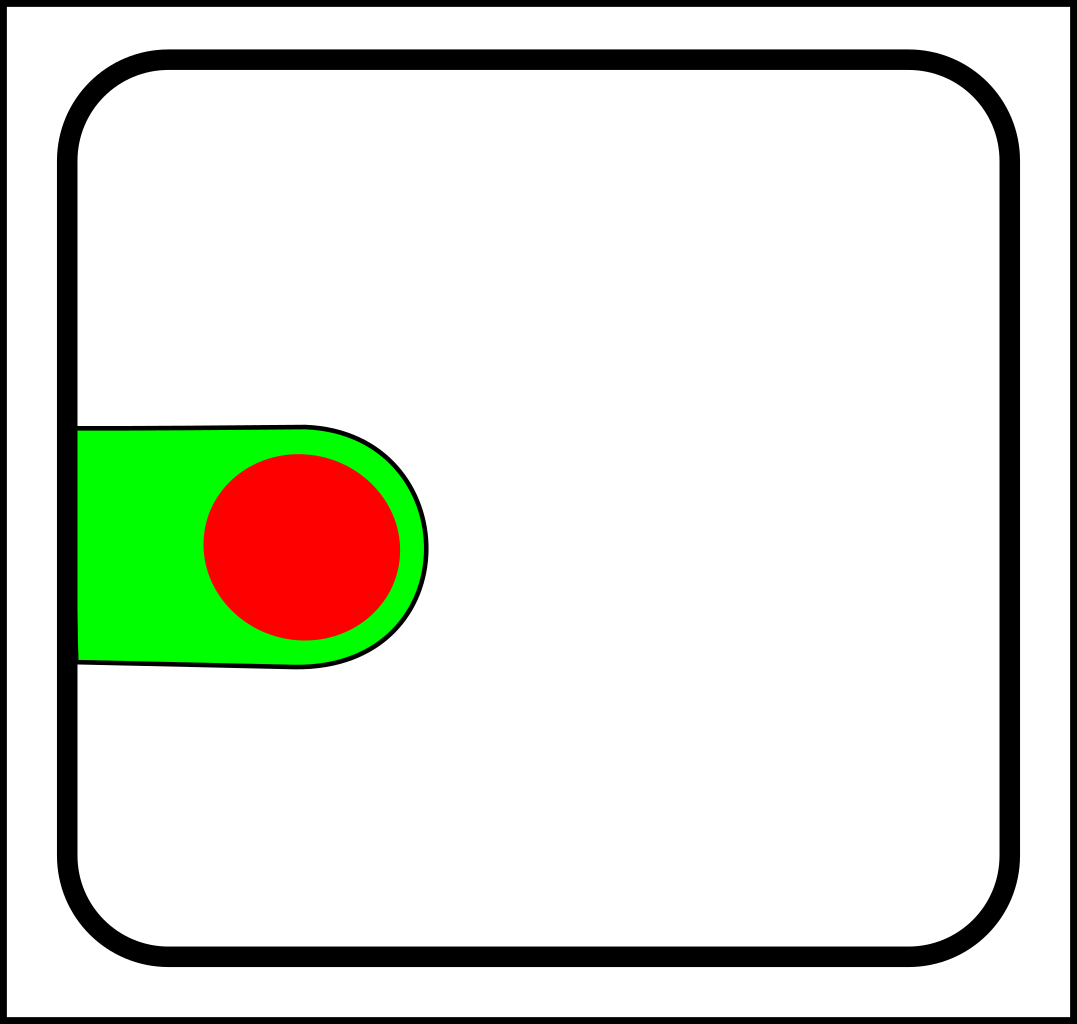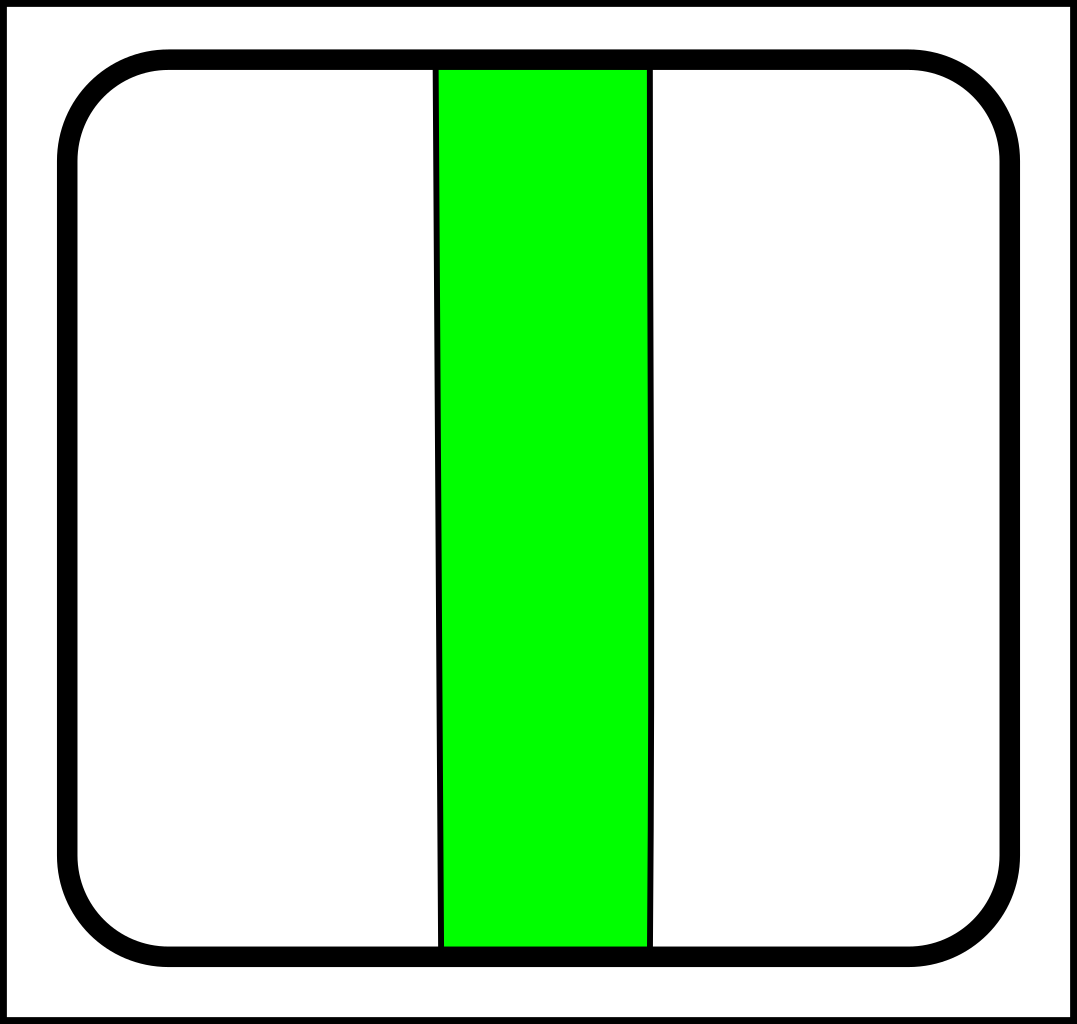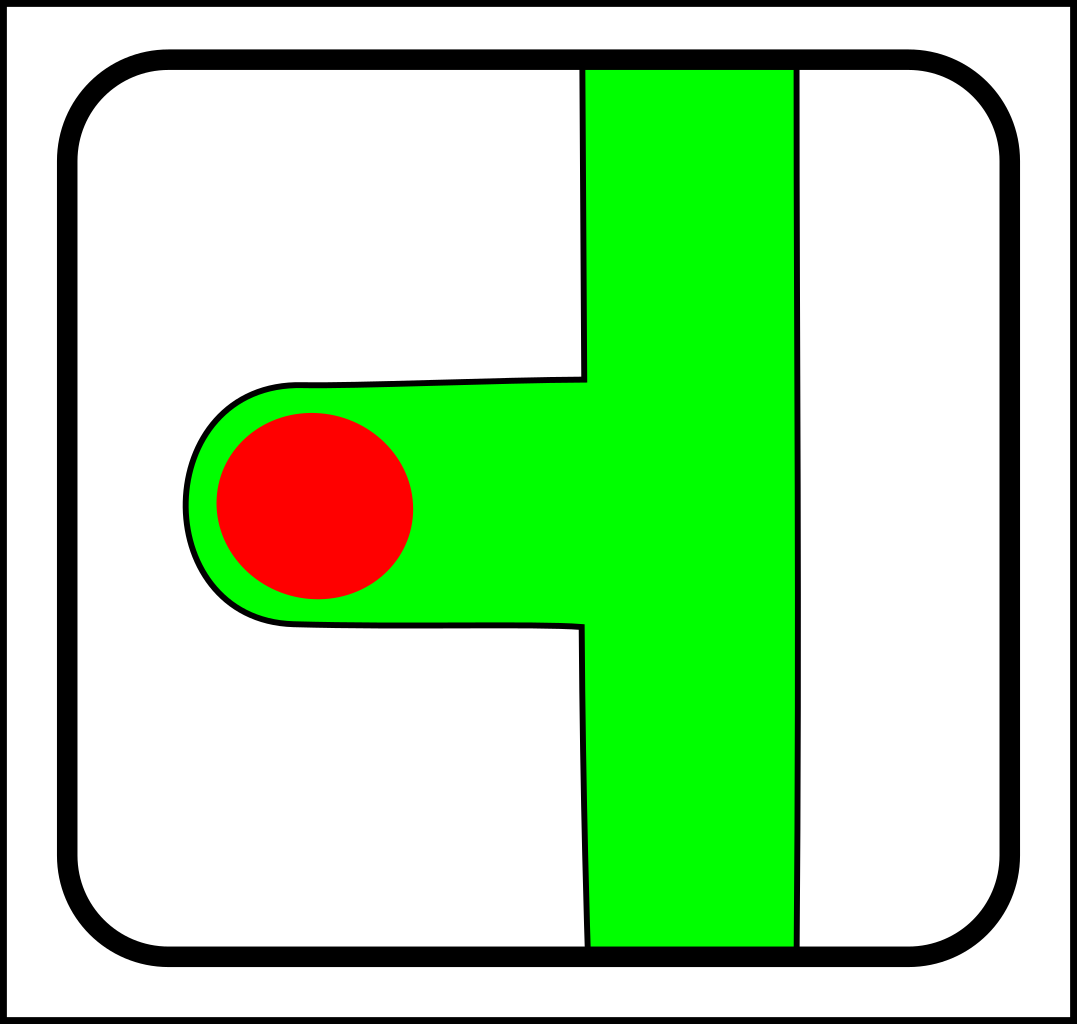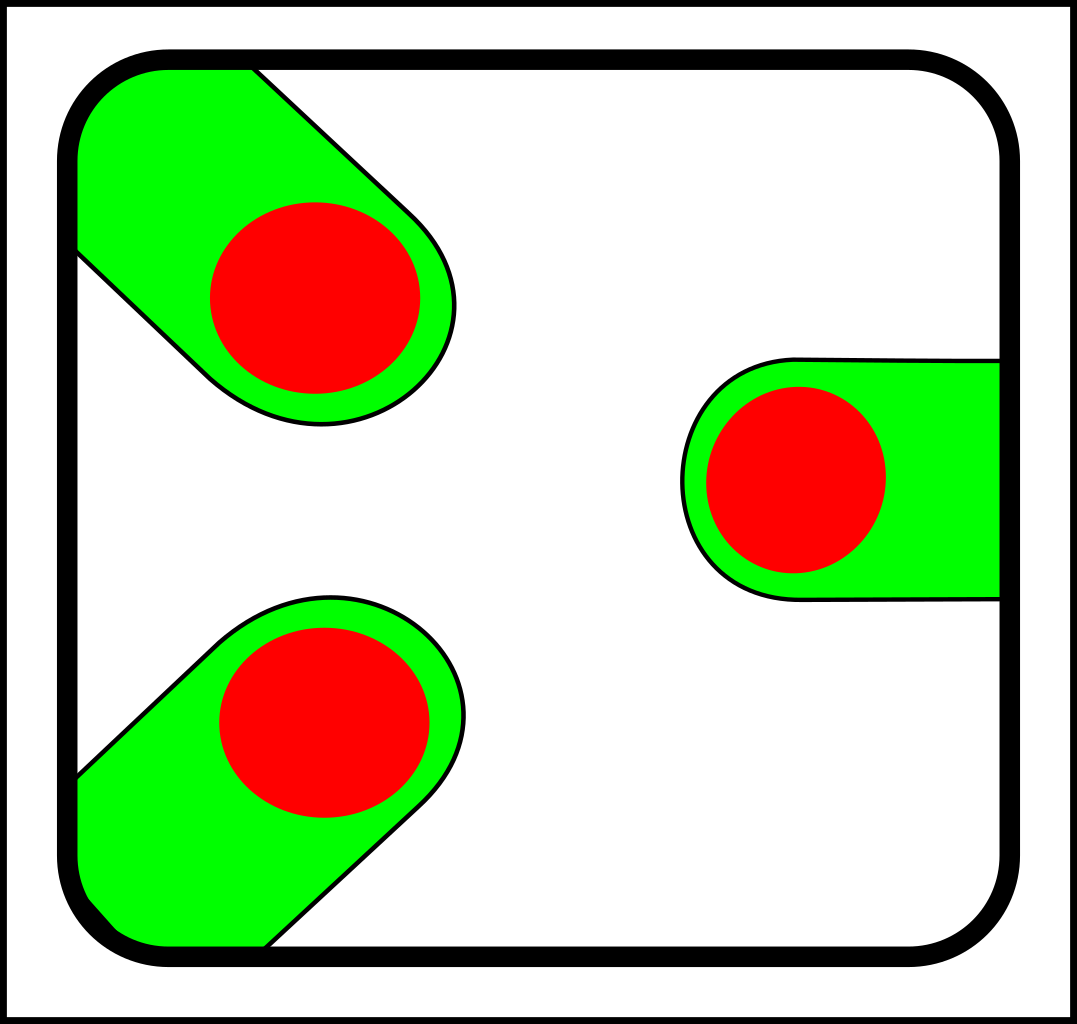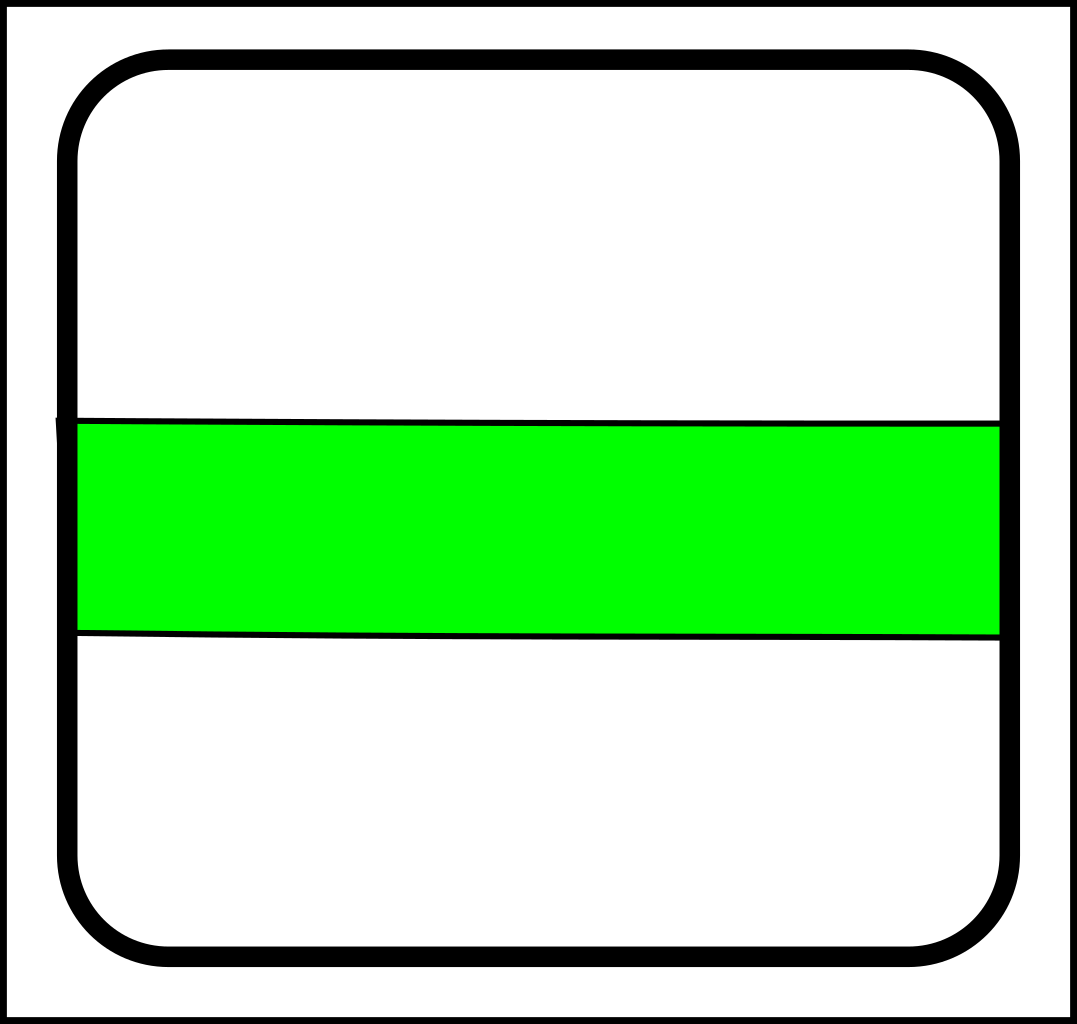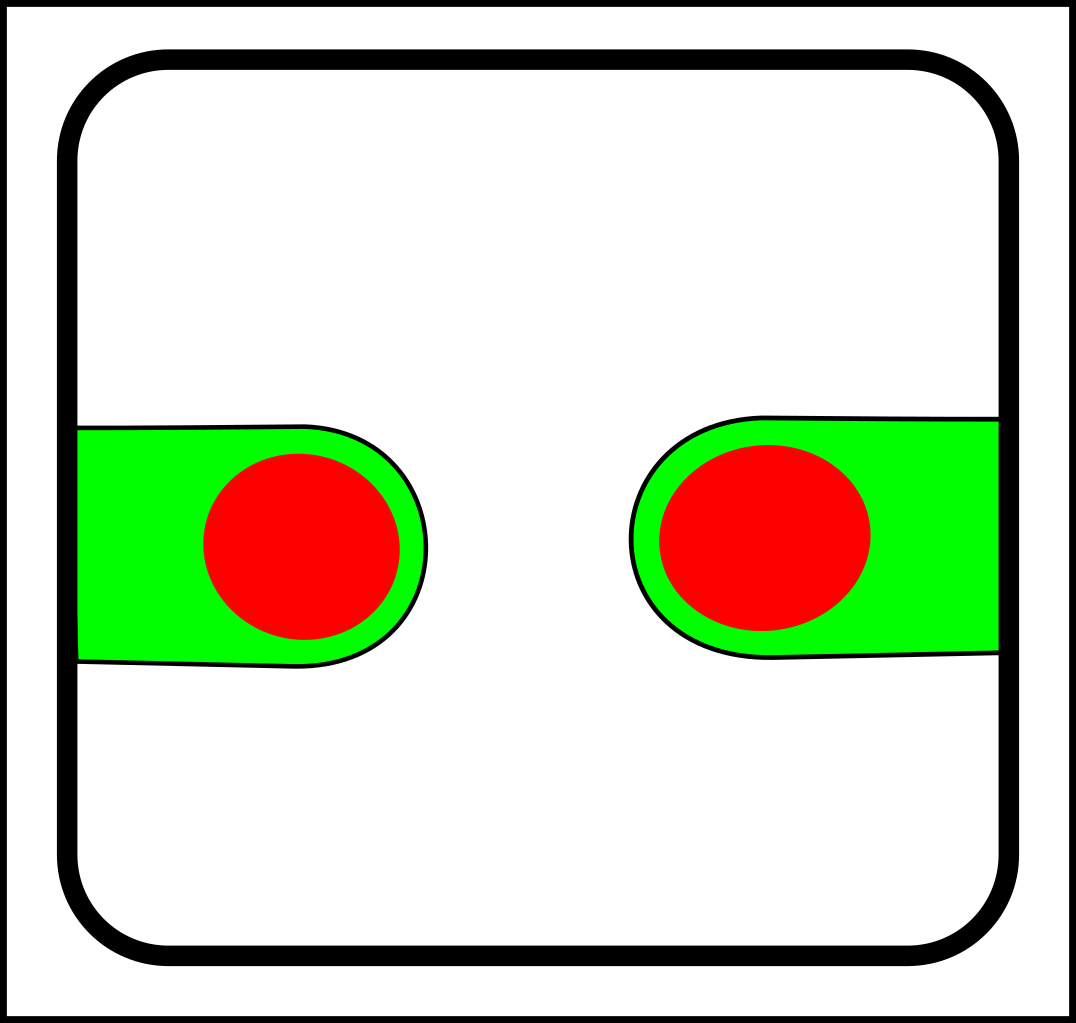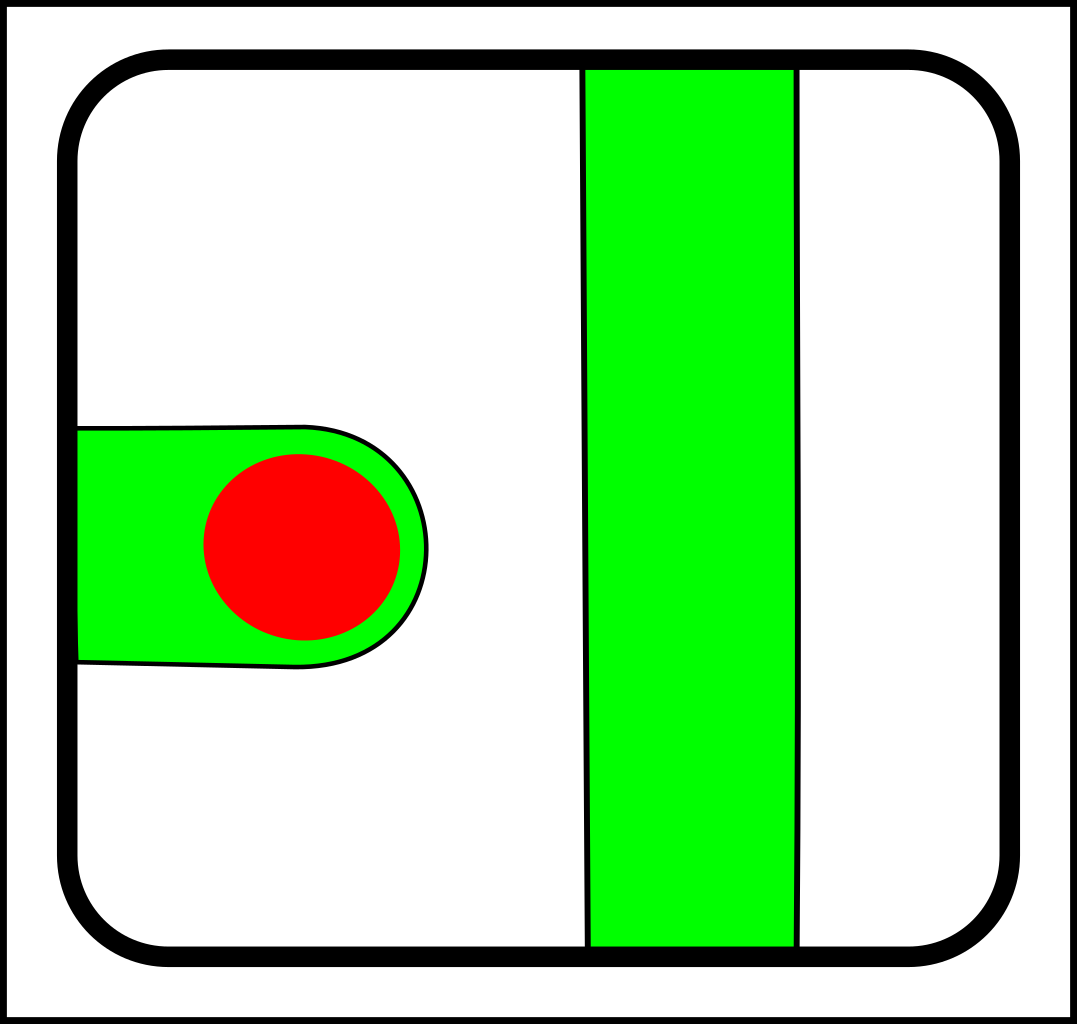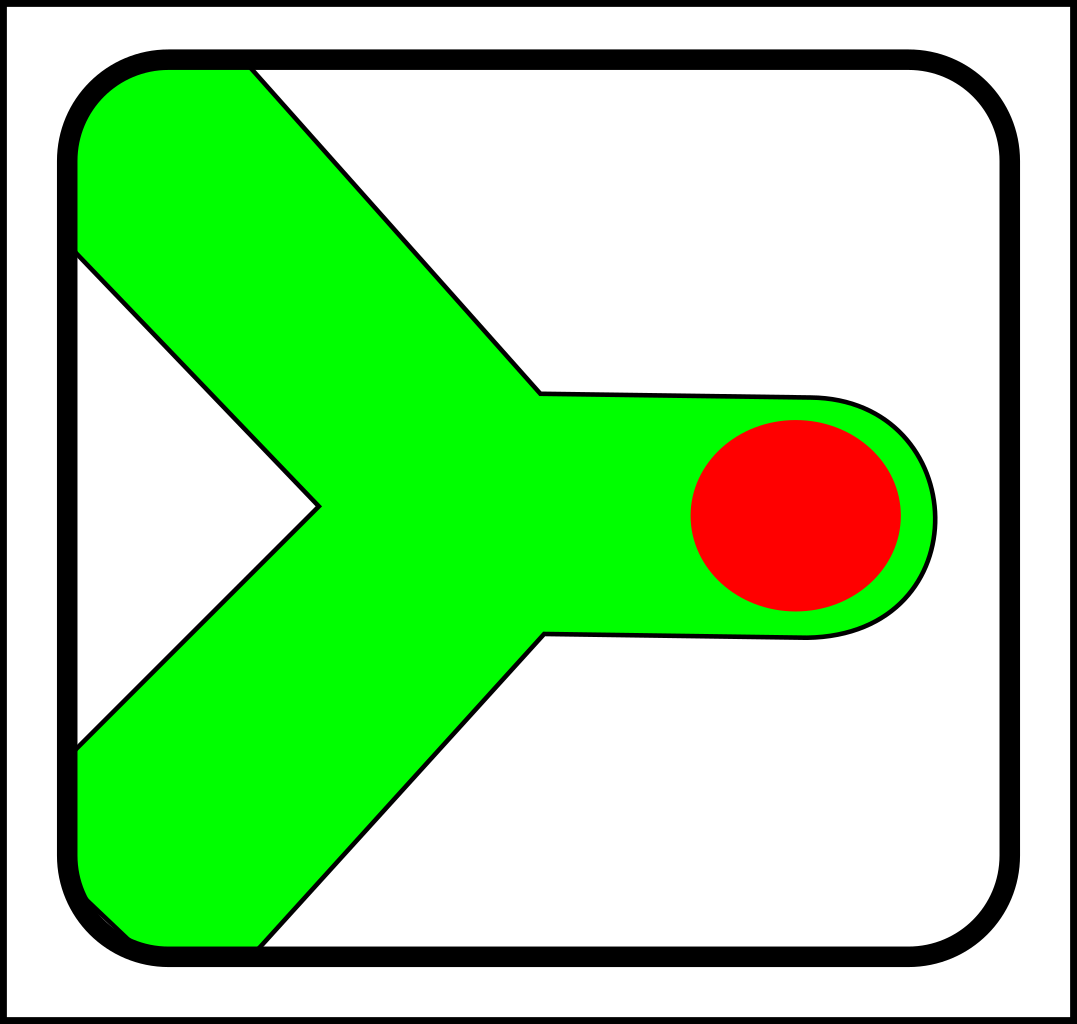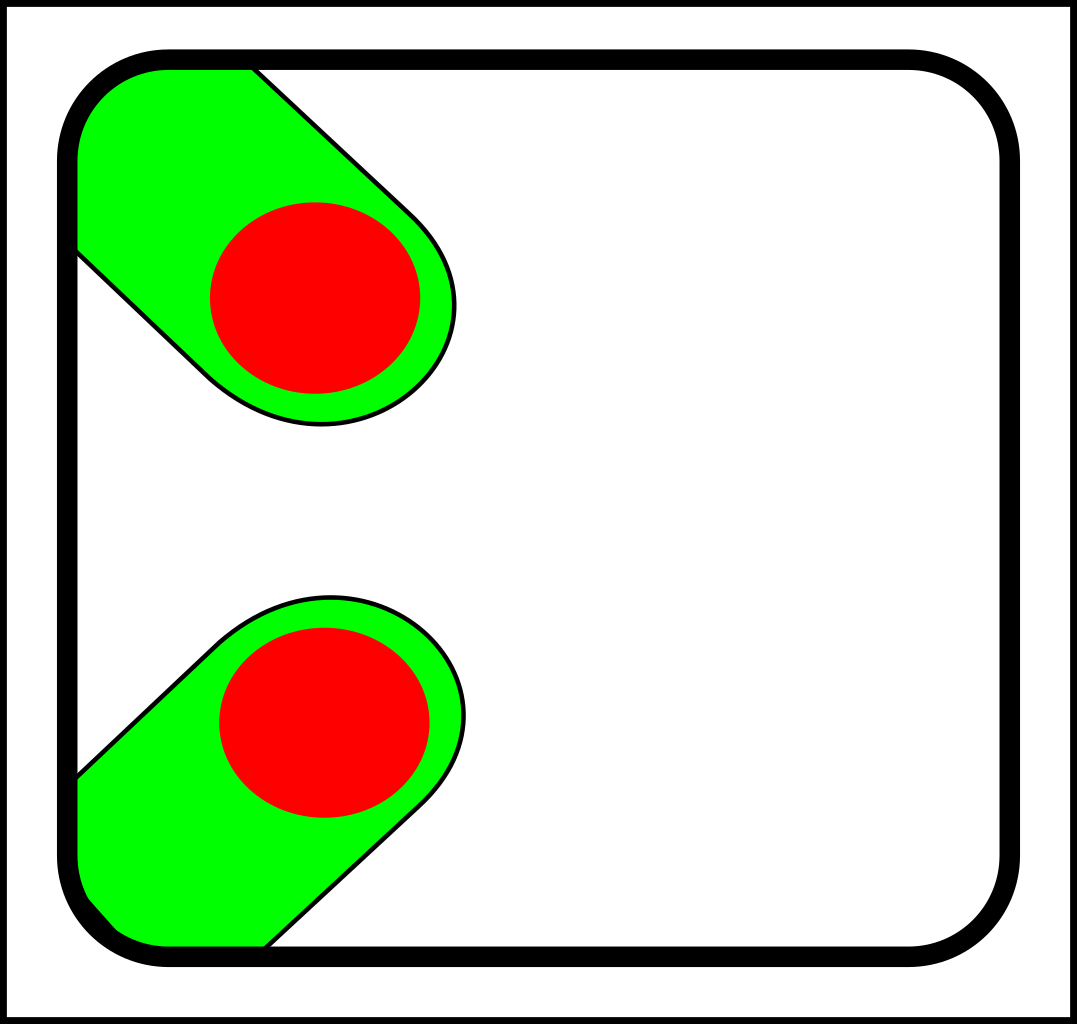...and here are the corresponding joining operations:

	->

	->

	->

	->

	->

	->

For the sake of simplicity, I've only shown diagrams for nodes with fewer than four links. I've also omitted selection events - i.e cases where elements (nodes or links) are simply destroyed.

I should probably say a bit more about the motivation for such a scheme. In biology, tree and graph evolution is often reducible to particle evolution - since the components involved are often composed of particulate cells. However, this doesn't work so well for brain evolution - since axons and dentrites are so link-like.

It's often possible to model branch tip evolution using conventional Darwinian models which treat branch tips as individuals. This works quite well in many of the types of inanimate systems considered by Darwinian physics, for example. However this approach works best when flow into the resulting tree-like structures is time-like - i.e. unidirectional and at a constant speed. If resources can flow back out of unpromising roots or newly-shaded branches, conventional Darwinian models based on a population of branch tips do not work so well. Then, more sophisticated models can be useful.

There is a field called evolutionary graph theory - but that seems to be about something rather different from the topic of this page.

Addy Pross vs universal Darwinism

I just noticed that Addy Pross offered a criticism of universal Darwinism in 2011:

we routinely attempt to explain psychological phenomena in biological terms, biological phenomena in physical and chemical terms, chemical phenomena in physical terms, and so on, not the other way around. The observation of Darwinian-like behavior at the chemical level is highly significant, not because it suggests that molecules behave in a biological fashion, but because it opens up the possibility of explaining biological behavior in chemical terms

Addy goes on to say:

As mentioned above, the temptation to interpret the behavior of molecular replicators in biological terms - fitness, natural selection, survival of the fittest, etc., should be firmly resisted. Chemical phenomena are more usefully explained in chemical terms

My response would be that this line of argument is based on a misidentificaton of where evolutionary theory lies in the scientific pecking order. It is true that evolutionary theory is used in biology - but it is more properly identified with statistics - in particular with statistical mechanics. This puts it above physics - along with systems theory, chaos theory, information theory, statistical thermodynamics and other theories that transcend physical law.

Addy's proposal that we should start with chemistry is a complete non-starter - since any chemical explanation would rather obviously fail to explain how Darwinism applies to physics and computer science.

Hitchhiking memes

I'm often on the lookout for opportunities to get memetics-related content to go viral on the internet. One potentially explosive topic is memetic hitchhiking. Memetic hitchhiking and memetic linkage are important topics for understanding memetics, but so far they have poor coverage in academia and online. I seem to be the main promotor of these concepts.

One thing I figure I can do to help is to make the proposed terminology as polished as possible. In my original memetic hitchhiking article I used the term 'payload' to describe content that spread via memetic linkage with another meme. That seems reasonable if the context is already memetic hitchhiking - but otherwise it is too vague. Enter hitchhiking memes:

"Hitchhiking meme" definition: a meme which spreads primarily via memetic linkage to another meme.

Meme-savvy marketers are probably the #1 audience for the memetic hitchhiking concept. It is a common marketing technique to link a brand or product with some viral content to help distribute it. The basic idea of memetic hitchhiking is pretty obvious, but the terminology to describe it scientifically is not getting used. My hope is that the idea of hitchhiking memes will give memetic hitchhiking a boost.